Up Board Exam 2026 Latest Model Paper 2026- Class 10 Maths – Based on New Education Policy – कक्षा 10 गणित मॉडल पेपर 2026 अब ऐसा पेपर आयेगा 2026 में –

हेलो फ्रेंड्स अगर आप भी क्लास 10 में पढ़ रहे हैं और अपनी परीक्षा की तैयारी के लिए मॉडल पेपर ढूंढ रहे हैं,तो आप सही जगह आये है यह आपको यूपी बोर्ड कक्षा 10 गणित परीक्षा 2026 के लिए प्रस्तुत है नवीनतम मॉडल पेपर, जो नई शिक्षा नीति पर आधारित है। इस पोस्ट में आपको मिलेगा नया प्रश्न प्रारूप, महत्वपूर्ण टॉपिक्स और स्मार्ट तैयारी। जानिए अब कैसा आएगा पेपर और करें परीक्षा की पक्की तैयारी!

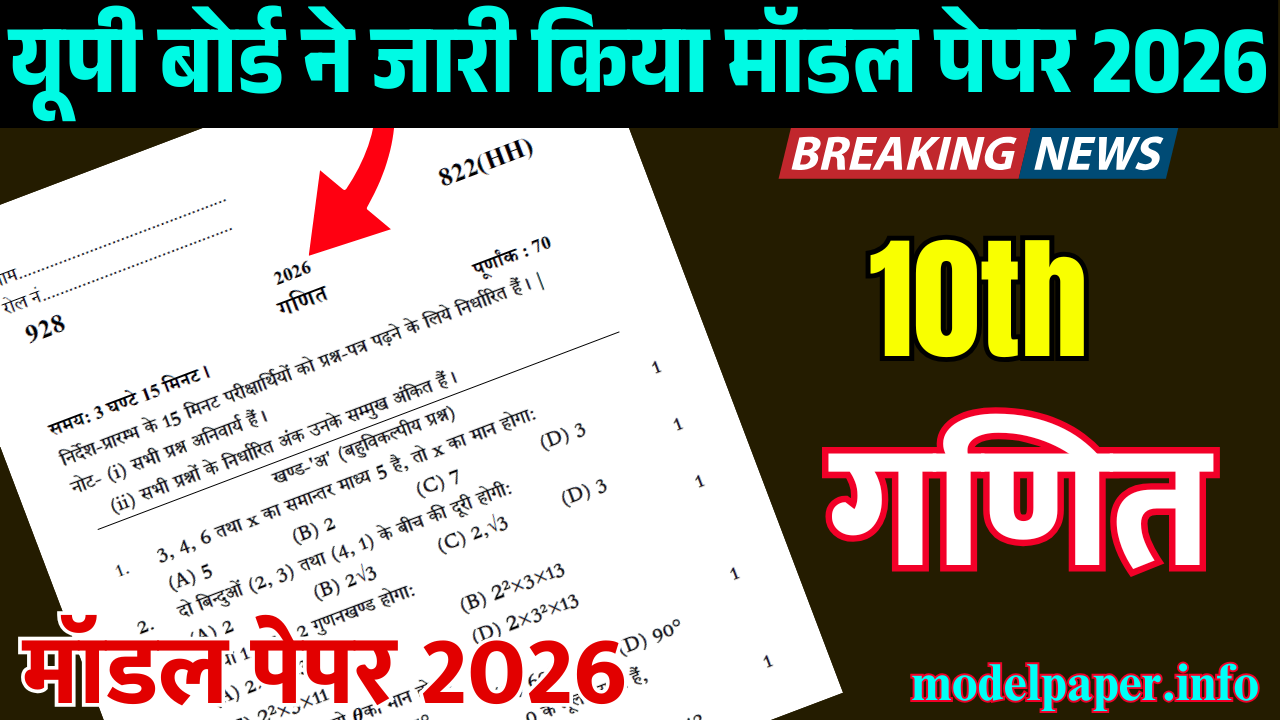
यदि आप Class 12th Maths Board Exam 2026 में अच्छे अंक लाना चाहते हैं तो इस नए मॉडल पेपर को जरूर देखें।

नाम………………………………………..

रोल नं…………………………………….

928 822(HH)

2026

गणित

समय: 3 घण्टे 15 मिनट । पूर्णांक : 70

निर्देश-प्रारम्भ के 15 मिनट परीक्षार्थियों को प्रश्न-पत्र पढ़ने के लिये निर्धारित हैं। |

नोट- (i) सभी प्रश्न अनिवार्य हैं।

(ii) सभी प्रश्नों के निर्धारित अंक उनके सम्मुख अंकित हैं।

खण्ड-‘अ’ (बहुविकल्पीय प्रश्न)

3, 4, 6 तथा x का समान्तर माध्य 5 है, तो x का मान होगा: 1

(A) 5 (B) 2 (C) 7 (D) 3

दो बिन्दुओं (2, 3) तथा (4, 1) के बीच की दूरी होगी: 1

(A) 2 (B) 2√3 (C) 2,√3 (D) 3

संख्या 156 का 2 गुणनखण्ड होगा: 1

(A) 2 3 13 (B) 2² 3 13

(C) 2² 3 11 (D) 2 3² 13

यदि secΘ = 2 तो का मान होगा: 1

(A)30° (B) 45° (C) 60° (D) 90°

यदि द्विघात समीकरण 3x² – 12x + m = 0 के मूल बराबर हैं, तो m का मान होगाः 1

(A) 4 (B) 7 (C) 9 (D) 12

एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्ष लम्ब की लम्बाई होगी : 1

(A) a (B) 2a√3 (C)a (D) 3a

समान्तर श्रेणी 2,4,6……7वाँ पद होगा 1

(A) 1 4 (B) 12 (C) 16 (D) 10

त्रिकोण (TRIANGLE) शब्द से व्यंजन चुनने की प्रायिकता होगी: 1

(A) 7/2 (B) 3/8 (C) 1/8 (D) 5/8

यदि शंकु की ऊर्ध्वाधर ऊँचाई और आधार का व्यास क्रमशः 15 सेमी व 16 सेमी हैं, तो शंकु का वक्रपृष्ठ होगा: 1

(A) 60 सेमी² (B) 68 सेमी² (C) 120 सेमी² (D) 136 सेमी²

वृत्त का क्षेत्रफल 64 सेमी² हो, तो उसका परिमाप होगा: 1

(A) 7 सेमी (B) 16 सेमी (C) 16 सेमी (D) 21 सेमी

यदि त्रिभुजों ABC तथा DEF में = हो, तो वह समरूप होंगे, यदि: 1

(A) ∠B = ∠ E (B) ∠A = D

(C) ∠B = ∠ D (D) ∠A = ∠ F

यदि वृत्त की परिधि 88 सेमी है, तो उसका व्यास होगा: 1

(A) 26 सेमी (B) 36 सेमी (C) 28 सेमी (D) 30 सेमी

यदि किसी त्रिभुज की भुजाएँ 3 सेमी, 4 सेमी और 5 सेमी हो, तो वह त्रिभुज होगा: 1

(A) समकोण त्रिभुज (B) न्यूनकोण त्रिभुज

(C) अधिक कोण त्रिभुज (D) त्रिभुज सम्भव नहीं

समीकरण x²-2x + 1 = 0 के मूल होंगे: 1

(A) 1,1 (B) 1, -1 (C) 2,-2 (D) 2, 2

यदि वृत्त की परिधि 44 सेमी है, तो त्रिज्या होगी: 1

(A) 7.5 सेमी (B) 7 सेमी (C) 3.5 सेमी (D) 14 सेमी

एक शंकु की ऊँचाई 12 सेमी एवं त्रियक ऊँचाई 13 सेमी हो, तो शंकु की त्रिज्या होगी: 1

(A) 4 सेमी (B) 6 सेमी (C) 5 सेमी (D) 7 सेमी

संख्याओं 1, 2, 3, 4, 5, 6 में सम संख्या आने की प्रायिकता होगी: 1

(A) 1/2 (B) 1/6 (C) 4/6 (D) इनमे से कोई नही

cos²Θ + 1/1+cot²Θ का मान होगा: 1

(A)0 (B) 2 (C) 1 (D) -1

2 सेमी वाले घन का वक्रपृष्ठ होगा: 1

(A) 8 सेमी² (B) 4 सेमी^² (C) 2 सेमी² (D) इनमें से कोई नहीं

दो लगातार संख्याओं का म०स० होगा: 1

(A) 2 (B) 4 (C) 6 (D) 1

👉 यहां से डाउनलोड करें और जानें कि 2026 में बोर्ड परीक्षा का पेपर कैसा आ सकता है। click here

खण्ड-‘ब’ (विस्तृत उत्तरीय प्रश्न)

सभी खण्ड कीजिए:

(क) अभाज्य गुणनखण्ड विधि द्वारा 96 और 404 का HCF और LCM ज्ञात कीजिए। 2

(ख) द्विघात समीकरण ज्ञात कीजिए जिसके मूल 3 और 1/3 हों। 2

(ग) एक बेलन के आधार की त्रिज्या 4 सेमी और ऊँचाई 14 सेमी है। बेलन का वक्रपृष्ठ क्षेत्रफल ज्ञात कीजिए? 2

(घ) एक समकोण त्रिभुज का क्षेत्रफल 30 सेमी² है। यदि उसकी ऊँचाई आधार की लंबाई से 7 सेमी अधिक है तो आधार की लंबाई ज्ञात कीजिए। 2

(ङ) 6 मीटर लम्बाई वाले एक ऊर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4 मीटर है, जबकि उसी समय एक मीनार की छाया की लम्बाई 28 मीटर है। मीनार की ऊँचाई ज्ञात कीजिए। 2

(च) यदि sin = 5/13 तो, 5sinΘ +4cosΘ/ 5sinΘ +4cosΘ का मान ज्ञात कीजिए। 2

निम्नलिखित में से किन्हीं पाँच खण्डों को हल कीजिए:

(क) ऐसे दो क्रमागत विषम धनात्मक पूर्णांक ज्ञात कीजिए, जिनके वर्गों का योगफल 290 हो। 4

(ख) एक लम्बवृत्तीय शंकु की तिर्यक ऊँचाई 13 सेमी तथा सम्पूर्ण पृष्ठ 90 सेमी है। इसके आधार की त्रिज्या ज्ञात कीजिए। 4

(ग) एक ठोस खिलौना एक अर्द्धगोले के आकार का है जिस पर एक लम्बवृत्तीय शंकु अध्यारोपित है। इस शंकु की ऊँचाई 2 सेमी है और आधार का व्यास

4 सेमी है। इस खिलौने का आयतन ज्ञात कीजिए। यदि एक लम्बवृत्तीय बेलन इस खिलौने के परिगत हो तो बेलन और खिलौने के आयतनों का अन्तर ज्ञात कीजिए। ( pi = 3.14 लीजिए) 4

(घ) पानी की सतह से 14 मीटर ऊपर जहाज के डेक पर खड़े एक व्यक्ति का एक पहाड़ी की चोठी से उन्नयन कोण 60° तथा पहाड़ी के आधार से अवनमन कोण 30° है। पहाड़ी की ऊँचाई तथा उसकी जहाज से दूरी ज्ञात कीजिए। (दिया गया है √3= 1.732) 4

(ङ) 10 मी ऊँचे भवन के शिखर से एक केबल टावर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टावर की ऊँचाई ज्ञात कीजिए

(√3= 1.73 का प्रयोग कीजिए)। 4

(च) निम्नांकित बंटन की माध्य ज्ञात कीजिए: 4

वर्ग-अन्तराल	10-10	10-20	20-30	30-40	40-50	50-60
बारम्बारता	7	12	18	15	10	3

एक नाव पुल की ओर आ रही है; किसी क्षण पुल का उन्नयन कोण 30° देखा गया। नाव के उसी चाल से 4 मिनट चलने के पश्चात पुल का उन्नयन कोण 60° हो गया। नाव को पुल तक पहुँचने में कितना समय और लगेगा? 6

अथवा

एक मीनार के आधार से 100 मीटर और 25 मीटर दूर उसी समतल पर स्थित दो बिन्दुओं A और B जो एक ही सीधी रेखा में हैं, उन पर मीनार के उन्नयन कोण एक दूसरे के कोटिपूरक हैं। मीनार की ऊँचाई ज्ञात कीजिए। 6

एक समकोण त्रिभुज की समकोण बनाने वाली भुजाएँ 5x और (3x-1) हैं तथा त्रिभुज का क्षेत्रफल 60 सेमी² है, तो त्रिभुज की भुजाएँ ज्ञात कीजिए। 6

अथवा

3 सेमी त्रिज्या वाले एक लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल 47.1 सेमी वर्ग है. शंकु का आयतन ज्ञात कीजिए। 6